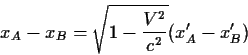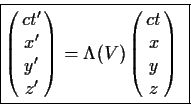

Next: Σύνθεση ταχυτήτων
Up: No Title
Previous: Τα σχετικιστικά φαινόμενα στην
Θεωρείστε δύο παρατηρητές Σ και Σ' με σχετική ταχύτητα V,
όπως δείχνει το σχήμα.
Σχήμα 8: Οι Σ και Σ' με σχετική ταχύτητα V.
Οι Σ και Σ' προκειμένου να περιγράψουν τα διάφορα γεγονότα,
έχουν ορίσει ο καθένας ένα σύστημα συντεταγμένων για τον
προσδιορισμό της θέσης στο χώρο και είναι
εφοδιασμένοι με ιδανικά ρολόγια για να περιγράφουν την
χρονική στιγμή που έλαβε χώρα το κάθε γεγονός.
'Ετσι, ο Σ χαρακτηρίζει τα διάφορα
γεγονότα με τις χωροχρονικές συντεταγμένες τους
(x,y,z,t) και ο Σ' με τις
(x',y',z',t').
Κάποιο γεγονός Α θα χαρακτηρίζεται με τις
συντεταγμένες
(xA,yA,zA,tA) από τον Σ και με τις
(x'A,y'A,z'A,t'A) απο τον Σ'.
Για να μπορούν οι δύο παρατηρητές να επικοινωνήσουν και να
συγκρίνουν τα αποτελέσματά τους, πρέπει να γνωρίζουν πώς
οι συντεταγμένες
(x',y',z',t') ενός
οποιουδήποτε γεγονότος σχετίζονται με τις
(x,y,z,t).
Οι σχέσεις αυτές ονομάζονται μετασχηματισμός Lorentz και
με την απόδειξή τους θα ασχοληθούμε στο κεφάλαιο αυτό.
Χωρίς βλάβη της γενικότητας μπορώ να ορίσω τις κατευθύνσεις
των αξόνων x και χ' να συμπίπτουν με την κατεύθυνση της
σχετικής ταχύτητας των Σ και Σ'. Μπορώ, επίσης χωρίς βλάβη της
γενικότητας, να φροντίσω ώστε τη στιγμή που ο παρατηρητής Σ'
περνάει μπροστά από τον Σ, και συμπίπτουν οι αρχές των αξόνων τους
να βάλουνε τα ρολόγια τους να δείχνουν t=0=t'.
'Eτσι, η "σύμπτωση των αρχών των αξόνων" αποτελεί ένα γεγονός
που χαρακρηρίζεται απο τις συντεταγμένες
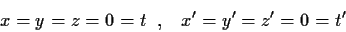 |
(22) |
κατά τους παρατηρητές Σ και Σ' αντίστοιχα.
Τα αποτελέσματα των προηγούμενων κεφαλαίων μας υποδεικνύουν
να αναζητήσομε μετασχηματισμό των συντεταγμένων ανάμεσα
στα Σ και Σ' που να είναι γραμμικός, και που για να
ικανοποιεί την (22) θα γράφεται στη μορφή
9
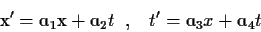 |
(23) |
με τις παραμέτρους
α1,α2,α3,α4, που μένει να
προσδιοριστούν, να εξαρτώνται μόνο
απο την σχετική ταχύτητα V των Σ και Σ'.
Οι παράμετροι υπολογίζονται ως εξής:
(α) Μάθαμε παραπάνω, οτι αν έχω δύο γεγονότα Α και Β που
συμβαίνουν στην ίδια θέση, ας πούμε ως προς τον παρατηρητή Σ,
δηλαδή χΑ=χΒ, τότε οι χρονικές αποστάσεις
t'A-t'B και tA-tB ικανοποιούν τη σχέση:
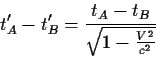 |
(24) |
Εφαρμόζω την δεύτερη απο τις (23) για τα δύο αυτά γεγονότα
και παίρνω:
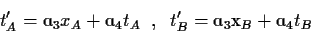 |
(25) |
Aφαιρώντας κατά μέλη και συγκρίνοντας με την (24) συμπεραίνω οτι
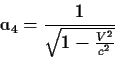 |
(26) |
(β) Αντίστοιχα, ας θεωρήσομε τη μέτρηση στο σύστημα Σ
του μήκους μιας ράβδου ακίνητης ως προς τον Σ', που
κατά συνέπεια κινείται ως προς τον Σ με ταχύτητα V.
Η κατάσταση περιγράφεται στο Σχήμα 9.
Σχήμα 9: Η μέτρηση του μήκους κινούμενης ράβδου.
Η μέτρηση γίνεται ως εξής: Τοποθετούμε παρατηρητές ακίνητους
κατά μήκος του άξονα των χ στο Σ με τα ρολόγια τους συγχρονισμένα,
και τους δίνομε την εξής εντολή: Σε κάποια χρονική στιγμή, ας πούμε οταν
τα ρολόγια τους δείχνουν 12:00, να σηκώσουν τα χέρια τους εκείνοι οι
δύο που έχουν μπροστά τους τα δύο άκρα της ράβδου. Αν χΑ και χΒ
είναι οι συντεταγμένες των δύο αυτών, τότε το μήκος της ράβδου
στο σύστημα αναφοράς Σ θα είναι
Eφαρμόζοντας την πρώτη απο τις (23) στα γεγονότα
"σύμπτωση του άκρου Α με τον παρατηρητή στο Α" και
"σύμπτωση του άκρου Β με τον παρατηρητή στο Β" παίρνομε
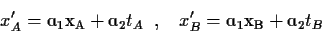 |
(28) |
Αφαιρούμε κατά μέλη, χρησιμοποιούμε την
tA=tB=12:00
και βρίσκομε
Η συστολή του μήκους που μάθαμε σε προηγούμενο κεφάλαιο
μας λέει οτι
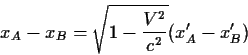 |
(30) |
απ' όπου καταλήγομε στην
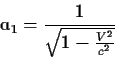 |
(31) |
(γ) Η ταχύτητα του φωτός είναι η ίδια ως προς κάθε αδρανειακό
παρατηρητή. Φανταστείτε οτι κατά τη στιγμή της σύμπτωσης των
αρχών των αξόνων των δύο συστημάτων άναψε μια φωτεινή πηγή
τοποθετημένη στην κοινή αρχή των αξόνων. Το προς τα δεξιά
διαδιδόμενο μέτωπο του
κύματος που εξέπεμψε η πηγή αυτή ικανοποιεί τις
εξισώσεις
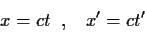 |
(32) |
ως προς τα συστήματα Σ και Σ', αντίστοιχα.
Μ'άλλα λόγια, αν τα χ και t ικανοποιούν την χ=ct, τα χ' και t'
που υπολογίζονται απο την (23) πρέπει να
ικανοποιούν την χ'=ct'.
Παίρνομε με αυτό το τρόπο τη σχέση
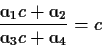 |
(33) |
(δ) Τέλος, η αρχή των αξόνων (χ'=0) του συστήματος Σ' όπως την παρατηρεί
ο Σ ικανοποιεί την εξίσωση
'Αρα, για κάθε t ισχύει
0=α1 χ+ α2 t=(α1 V + α2)t, και επομένως
οι παράμετροι ικανοποιούν και τη σχέση
Απο τις (26), (31), (33) και (35)
παίρνομε
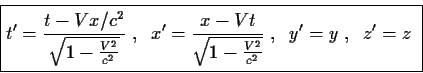 |
(36) |
Aυτός είναι ο μετασχηματισμός Lorentz που συνδέει δύο συστήματα
αναφοράς Σ και Σ', όπως δείχνει το Σχήμα 8.
Ισοδύναμα, κάνοντας χρήση του κανόνα πολλαπλασιασμού πινάκων,
εύκολα μπορείτε να επαληθεύσετε οτι
ο μετασχηματισμός Lorentz (36)
κατά την
κατεύθυνση χ που περιοριστήκαμε εδώ, γράφεται και στη μορφή
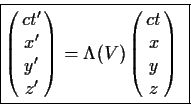 |
(37) |
με τον πίνακα Lorentz
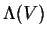
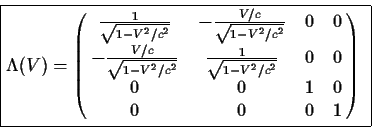 |
(38) |
Η γενίκευση των παραπάνω για σχετική κίνηση σε τυχούσα κατεύθυνση και γενικό
σχετικό προσανατολισμό των δύο συστημάτων είναι εύκολη αλλά
όχι απαραίτητη για τις ανάγκες του μαθήματος.
Σχόλιο 1: Ο μετασχηματισμός Γαλιλαίου προκύπτει ως το όριο
V=σταθερό και
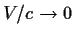 .
Πράγματι, στο όριο αυτό ο μετασχηματισμός
(36) γίνεται
.
Πράγματι, στο όριο αυτό ο μετασχηματισμός
(36) γίνεται
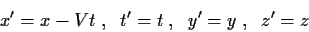 |
(39) |
H Νευτώνεια μηχανική περιγράφει ικανοποιητικά τα φαινόμενα
στο όριο των μικρών (ως προς την ταχύτητα του φωτός) ταχυτήτων.
Σχόλιο 2: Χρησιμοποιώντας τους τύπους (36) μπορείτε εύκολα
να επαληθεύσετε οτι ισχύει
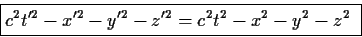 |
(40) |
Γενικώτερα, για δύο οποιαδήποτε γεγονότα οι χωροχρονικές τους
αποστάσεις ως προς δύο αδρανειακούς παρατηρητές ικανοποιούν τη
σχέση
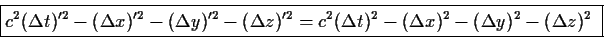 |
(41) |
Οι σχέσεις αυτές, που θα μας είναι πολύ χρήσιμες παρακάτω,
ισχύουν για οποιονδήποτε μετασχηματισμό Lorentz. 'Οχι μόνο
για αδρανειακούς παρατηρητές με σχετική ταχύτητα στην κατεύθυνση του
άξονα των χ.
Σχόλιο 3: Ο αντίστροφος του μετασχηματισμού (36), δηλαδή
οι σχέσεις που μας δίνουν τις χωροχρονικές συντεταγμένες ενός
γεγονότος στο σύστημα Σ απο αυτές στο σύστημα Σ', υπολογίζεται
επιλύοντας τις (36) ως προς x,t συναρτήσει των
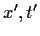 .
Θα βρείτε
.
Θα βρείτε
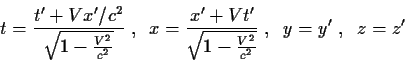 |
(42) |
'Ενας άλλος τρόπος να αποδείξει κανείς τις σχέσεις αυτές είναι να
σκεφτεί οτι αν για τον παρατηρητή Σ' ο Σ κινείται με ταχύτητα
V προς τα αριστερά στο Σχήμα 1, ο Σ βλεπει τον Σ' να κινείται
με ταχύτητα V προς τα δεξιά. 'Aρα παίρνομε τον μετασχηματισμό
από το σύστημα Σ' στο Σ αντικαθιστώντας το V στις (36)
με -V.
Αλλοιώς, μπορεί να σκεφτεί κανείς οτι γενικά, ο αντίστροφος ενός
μετασχηματισμού είναι ένας άλλος μετασχηματισμός που αν συνδυαστεί με τον
αρχικό, μας οδηγεί στος ταυτοτικό μετασχηματισμό, δηλαδή σε καθόλου αλλαγή
συστήματος. Το αποτέλεσμα ενός μετασχηματισμού Lorentz με ταχύτητα
V εξουδετερώνεται από άλλον με ταχύτητα -V.
Τέλος, για όσους προτιμάνε να σκέφτονται αλγεβρικά, απλά ας παρατηρήσουν
οτι
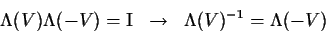 |
(43) |
όπου με Ι συμβολίσαμε τον πίνακα μονάδα.
Σχόλιο 4: Eίναι σημαντικό να αναφερθεί εδώ οτι με τον μετασχηματισμό
Lorentz (36) να συνδέει διαφορετικούς αδρανειακούς
παρατηρητές, οι νόμοι του Maxwell για τη διάδοση
της ηλεκτρομαγνητικής ακτινοβολίας είναι οι ίδιοι ως
προς όλους αυτούς τους παρατηρητές.
ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ. Στις σημειώσεις αυτές διαλέξαμε
να παρουσιάσομε την Ειδική Θεωρία της Σχετικότητας με την
βοήθεια απλών νοητικών πειραμάτων της μηχανικής, με τραίνα,
ράβδους και διαστημόπλοια. Ισοδύναμα, και πιό κοντά στο πώς
έγιναν τα πράγματα ιστορικά, μπορεί κανείς να ξεκινήσει
με την παρατήρηση οτι η θεωρία του Maxwell για την ηλεκτρομαγνητική
ακτινοβολία είναι αναλλοίωτη κάτω από μετασχηματισμούς
Lorentz και όχι Γαλιλαίου. Αν επομένως οι νόμοι της
ηλεκτρομαγνητικής ακτινοβολίας στο κενό είναι οι ίδιοι ως
προς όλους τους αδρανειακούς παρατηρητές, τότε πρέπει ο μετασχηματισμός
που συνδέει δύο αδρανειακούς παρατηρητές να είναι
ο μετασχηματισμός Lorentz.
Η μηχανική του Νεύτωνα όμως δεν είναι αναλλοίωτη ως προς
τον μετασχηματισμό Lorentz. Επομένως, ο μόνος τρόπος να ικανοποιήσομε
το αξίωμα της σχετικότητας είναι να αναδιατυπώσομε κατάλληλα
τους νόμους της μηχανικής. Αυτό ακριβώς είναι που θα κάνομε
στη συνέχεια.


Next: Σύνθεση ταχυτήτων
Up: No Title
Previous: Τα σχετικιστικά φαινόμενα στην
Konstantinos Anagnostopoulos
2002-03-13
![\includegraphics[width=12cm]{f09.eps}](img57.gif)
![\includegraphics[width=12cm]{f09.eps}](img57.gif)
![\includegraphics[width=12cm]{f10.eps}](img63.gif)