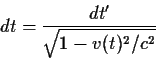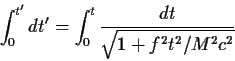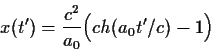

Next: Σκέδαση φωτονίων - Φαινόμενο
Up: Σχετικιστική κινηματική
Previous: Πυρηνικές διασπάσεις
Σώμα μάζας Μ βρίσκεται ακίνητο στην αρχή των αξόνων.
Τη χρονική στιγμή t=0 εφαρμόζομε πάνω του μια
σταθερή δύναμη f στην κατεύθυνση του άξονα των χ.
Να μελετηθεί η κίνησή του.
Το σκηνικό που περιγράφομε εδώ είναι μια καλή προσέγγιση για τη
μελέτη της κίνησης φορτίων σε ένα γραμμικό επιταχυντή, όπου
φορτισμένα σωμάτια (ηλεκτρόνια, ποζιτρόνια, πρωτόνια)
επιταχύνονται υπο την επίδραση
σταθερού ηλεκτρικού πεδίου.
To υπό μελέτην σώμα ξεκινά από την ηρεμία υπό την επίδραση δύναμης
στην κατεύθυνση χ. 'Ολη η κίνηση επομένως εξελίσσεται στην κατεύθυνση χ.
Οι χ και y συνιστώσες της ταχύτητας παραμένουν μηδέν.
Η εξίσωση κίνησης του σώματος ως προς το αδρανειακό σύστημα
του εργαστηρίου μας είναι
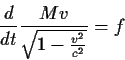 |
(81) |
όπου v η χ συνιστώσα της ταχύτητας του σώματος.
(α) Η ταχύτητα v(t). Ολοκληρώνω ως προς χρόνο από 0 μέχρι t
τα δύο μέλη της εξίσωσης αυτής και παίρνω
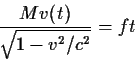 |
(82) |
ή ισοδύναμα
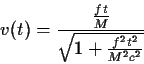 |
(83) |
Για μικρούς χρόνους, δηλαδή για
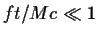 το σώμα δεν έχει ακόμα
αναπτύξει μεγάλη ταχύτητα, και επομένως ο παραπάνω τύπος ανάγεται όπως περιμέναμε
στο Νευτώνειο αποτέλεσμα
το σώμα δεν έχει ακόμα
αναπτύξει μεγάλη ταχύτητα, και επομένως ο παραπάνω τύπος ανάγεται όπως περιμέναμε
στο Νευτώνειο αποτέλεσμα
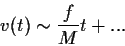 |
(84) |
Αντίστοιχα, για μεγάλους χρόνους
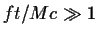 ,
η ταχύτητα πλησιάζει
ασυμπτοτικά την ταχύτητα του φωτός
,
η ταχύτητα πλησιάζει
ασυμπτοτικά την ταχύτητα του φωτός
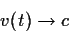 |
(85) |
(β) Η θέση χ(t) του σώματος. Η εξίσωση (81) γράφεται επίσης
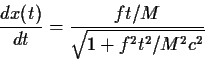 |
(86) |
από την οποία με ολοκλήρωση και των δύο μελών ως προς χρόνο παίρνομε
14
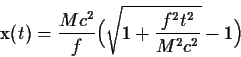 |
(87) |
Xρησιμοποιείστε το ανάπτυγμα Taylor
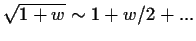 για
για 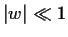 για να βεβαιωθείτε οτι για μικρούς χρόνους
για να βεβαιωθείτε οτι για μικρούς χρόνους
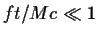 παίρνετε το
Νευτώνειο αποτέλεσμα
παίρνετε το
Νευτώνειο αποτέλεσμα
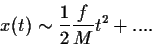 |
(88) |
Eπίσης, εύκολα μπορείτε να επαληθεύσετε οτι για μεγάλους χρόνους
η σχέση (85) γίνεται
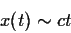 |
(89) |
όπως αναμενόταν.
(γ) Η επιτάχυνση a(t) του σώματος υπολογίζεται με μιά απλή
παραγώγιση της (81) ως προς τον χρόνο.
To αποτέλεσμα είναι:
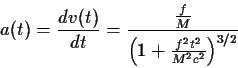 |
(90) |
Η επιτάχυνση ξεκινάει από την τιμή f/M για t=0 και τείνει στο μηδέν
σαν
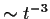 για μεγάλους χρόνους. Σταθερή δύναμη δεν συνεπάγεται σταθερή επιτάχυνση.
Κάτι τέτοιο θα είχε σαν αποτέλεσμα αργά ή γρήγορα το σώμα να ξεπεράσει
την ταχύτητα του φωτός.
Σχήμα 16: Οι γραφικές παραστάσεις των x(t), v(t) και a(t) σώματος υπό
την επίδραση σταθερής δύναμης στην κατεύθυνση χ. Το σώμα ξεκίνησε
από την ηρεμία στη θέση x=0.
για μεγάλους χρόνους. Σταθερή δύναμη δεν συνεπάγεται σταθερή επιτάχυνση.
Κάτι τέτοιο θα είχε σαν αποτέλεσμα αργά ή γρήγορα το σώμα να ξεπεράσει
την ταχύτητα του φωτός.
Σχήμα 16: Οι γραφικές παραστάσεις των x(t), v(t) και a(t) σώματος υπό
την επίδραση σταθερής δύναμης στην κατεύθυνση χ. Το σώμα ξεκίνησε
από την ηρεμία στη θέση x=0.
(δ) Η επιτάχυνση στο σύστημα ηρεμίας του σώματος. Τί επιτάχυνση
αισθάνεται το ίδιο το σώμα; 'Ενας παρατηρητής στο σύστημα ηρεμίας του
σώματος αντιλαμβάνεται μονίμως ένα ακίνητο σώμα υπο την επίδραση
μιας σταθερής δύναμης. 'Αρα ως προς αυτόν το σώμα έχει σταθερή
επιτάχυνση a0=f/M.
Πράγματι, στο αποτέλεσμα αυτό καταλήγει κανείς και ως εξής:
Το σύστημα ηρεμίας του σώματος ΔΕΝ είναι αδρανειακό. Αυτό είναι
φανερό, αφού το σώμα επιταχύνεται ως προς το αδρανειακό σύστημα
του εργαστηρίου μας. Την χρονική στιγμή t η ταχύτητα του σώματος
δίδεται απο τη σχέση (81).
Eπομένως, ένα σύστημα που κινείται κατά το χρονικό διάστημα
(t, t+dt) με τη σταθερή ταχύτητα v(t) είναι αδρανειακό
και για απειροστά μικρό dt συμπίπτει με το σύστημα ηρεμίας
του σώματος. Είναι αυτό που λέμε στιγμιαίο αδρανειακό σύστημα
ηρεμίας του σώματος.
Σχήμα 17: Το σύστημα Σ' είναι το στιγμιαίο αδρανειακό σύστημα ηρεμίας
του σώματος Α. To Σ είναι το αδρανειακό σύστημα του εργαστηρίου.
Η σχετική ταχύτητα των δύο συστημάτων είναι η στιγμιαία ταχύτητα
v(t) του σώματος.
H επιτάχυνση επομένως του Α ως προς εαυτόν υπολογίζεται από τον
τύπο (49), βάζοντας την σχετική ταχύτητα V=vχ(t), ίση δηλαδή
προς την στιγμιαία ταχύτητα του σώματος.
To αποτέλεσμα είναι
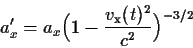 |
(91) |
Χρησιμοποιώντας τέλος την έκφραση (81) για την vx(t)
καταλήγομε στο οτι
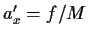 .
(ε) 'Ενα άλλο ενδιαφέρον ερώτημα είναι το εξής: Πόσος χρόνος
.
(ε) 'Ενα άλλο ενδιαφέρον ερώτημα είναι το εξής: Πόσος χρόνος
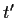 έχει περάσει σύμφωνα με το ρολόι του σώματος
μέχρι τη χρονική στιγμή t του ρολογιού στο εργαστήριο;
Πάρτε πάλι το στιγμιαίο αδρανειακό σύστημα ηρεμίας Σ' του σωματιδίου
το χρονικό διάστημα (t,t+dt) ως προς το εργαστήριο.
Στο χρονικό διάστημα dt του Σ αντιστοιχεί το
έχει περάσει σύμφωνα με το ρολόι του σώματος
μέχρι τη χρονική στιγμή t του ρολογιού στο εργαστήριο;
Πάρτε πάλι το στιγμιαίο αδρανειακό σύστημα ηρεμίας Σ' του σωματιδίου
το χρονικό διάστημα (t,t+dt) ως προς το εργαστήριο.
Στο χρονικό διάστημα dt του Σ αντιστοιχεί το 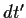 κατά τον Σ',
που δίδεται από τον τύπο της διαστολής του χρόνου
κατά τον Σ',
που δίδεται από τον τύπο της διαστολής του χρόνου
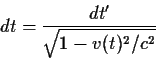 |
(92) |
Aντικαθιστώ την v(t) από την (81) και ολοκληρώνω στα
αντίστοιχα χρονικά διαστήματα (0,t) και
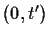 και
παίρνω
και
παίρνω
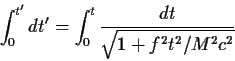 |
(93) |
με τελικό αποτέλεσμα τη σχέση
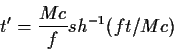 |
(94) |
(στ) Κοσμοναύτης παίρνει το διαστημόπλοιό του και με σταθερή επιτάχυνση
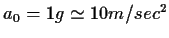 (όπως την αντιλαμβάνεται ο ίδιος)
κατευθύνεται προς την Ανδρομέδα που απέχει
από τη Γη 900000 έτη φωτός. Πόσο χρόνο θα χρειαστεί για να φθάσει στον
προορισμό του;
Zητάμε με άλλα λόγια τον χρόνο
(όπως την αντιλαμβάνεται ο ίδιος)
κατευθύνεται προς την Ανδρομέδα που απέχει
από τη Γη 900000 έτη φωτός. Πόσο χρόνο θα χρειαστεί για να φθάσει στον
προορισμό του;
Zητάμε με άλλα λόγια τον χρόνο 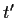 που θα χρειαστεί ο κοσμοναύτης
όπως τον μετράει ο ίδιος, για να διανύσει απόσταση χ=900000 έτη φωτός,
όπως τα μετράει ο αδρανειακός γήινος παρατηρητής.
Χρειαζόμαστε επομένως τη σχέση
που θα χρειαστεί ο κοσμοναύτης
όπως τον μετράει ο ίδιος, για να διανύσει απόσταση χ=900000 έτη φωτός,
όπως τα μετράει ο αδρανειακός γήινος παρατηρητής.
Χρειαζόμαστε επομένως τη σχέση
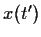 ,
που δίνει την απόσταση που
διανύει ο κοσμοναύτης (κατά τον Σ), σαν συνάρτηση του χρόνου
,
που δίνει την απόσταση που
διανύει ο κοσμοναύτης (κατά τον Σ), σαν συνάρτηση του χρόνου 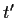 του Σ'.
Η απόσταση χ(t) που διανύει, σαν συνάρτηση του χρόνου του Γήινου παρατηρητή
δίδεται από τη σχέση (85).
Αντιστρέφοντας την (92) παίρνομε
του Σ'.
Η απόσταση χ(t) που διανύει, σαν συνάρτηση του χρόνου του Γήινου παρατηρητή
δίδεται από τη σχέση (85).
Αντιστρέφοντας την (92) παίρνομε
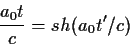 |
(95) |
την οποία αντικαθιστώντας στην (85) βρίσκομε
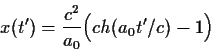 |
(96) |
Eφαρμογή: Για
a0=10m/sec2 και x=900000 έτη φωτός ο ζητούμενος
χρόνος είναι
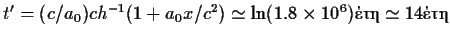 .
'Εχοντας, λοιπόν, σταθερή επιτάχυνση ίση προς την επιτάχυνση της βαρύτητας
στην επιφάνεια της γης μπορείτε να φτάσετε στην Ανδρομέδα, που απέχει
από τη γη 900000 έτη φωτός, σε μόλις 14 χρόνια!!
Κατά τον Νεύτωνα ο απαιτούμενος χρόνος για το ταξίδι αυτό
θα ήταν περισσότερα από 1000 χρόνια! Αποδείξτε το.
.
'Εχοντας, λοιπόν, σταθερή επιτάχυνση ίση προς την επιτάχυνση της βαρύτητας
στην επιφάνεια της γης μπορείτε να φτάσετε στην Ανδρομέδα, που απέχει
από τη γη 900000 έτη φωτός, σε μόλις 14 χρόνια!!
Κατά τον Νεύτωνα ο απαιτούμενος χρόνος για το ταξίδι αυτό
θα ήταν περισσότερα από 1000 χρόνια! Αποδείξτε το.


Next: Σκέδαση φωτονίων - Φαινόμενο
Up: Σχετικιστική κινηματική
Previous: Πυρηνικές διασπάσεις
Konstantinos Anagnostopoulos
2002-03-13
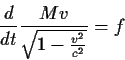
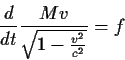
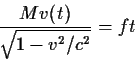
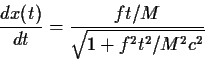
![\includegraphics[width=12cm]{xva.eps}](img172.gif)
![\includegraphics[width=12cm]{f23.eps}](img173.gif)